A zero-knowledge proof (ZKP) is a method of proving the validity of a statement without revealing anything other than the validity of the statement itself. It is a proof system with a prover, a verifier, and a challenge that gives users the ability to publicly share a proof of knowledge or ownership without revealing the details of it.

In cryptography, zero-knowledge proofs let you convince me that you know something, or have done something, without revealing to me what that secret thing was. It is one of the most powerful cryptographic tools that has ever been devised. In this article, we dive deeper into what zero-knowledge proofs are, and provide different examples to help you understand how they work.

The concept of a prover, a verifier, and the statement being proven

At the core of zero-knowledge proofs is a scenario involving two parties: the prover and the verifier. The prover aims to convince the verifier of the truthfulness of a statement without divulging any information that could be used to replicate or deduce the statement itself.

• Prover: This is the party holding some secret or information that needs to be verified. The prover aims to convince the verifier of a particular statement's truthfulness without revealing the actual information.

• Verifier: The verifier is the questioning party that requests proof from the prover. The verifier wants to be sure that the prover possesses the necessary information without learning anything beyond that.

• Statement: This refers to the assertion or claim that the prover aims to prove. It could be anything from knowledge of a password to possession of a private cryptographic key.

Example: Proof of Membership

Another way of thinking about zero-knowledge proofs is with this example of the locked safe.

You meet someone you do not know, yet she claims to also be a member of the group you are part of. How can you know if you can trust her? Luckily, your group has a locked safe, and only the members of your group know the secret combination code to gain access to the safe. So write a secret message and place it in the locked safe.

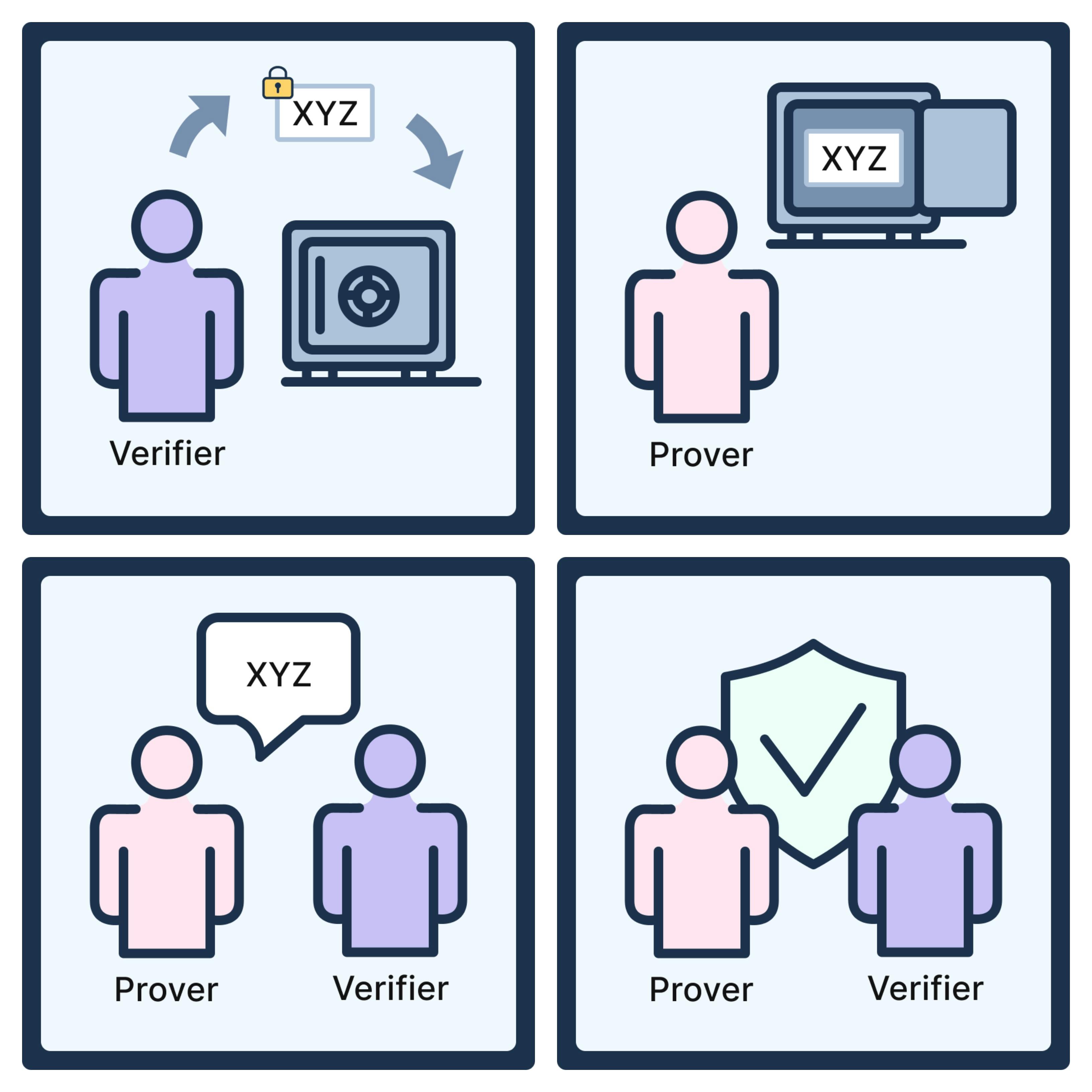
1. Verifier writes a secret message and put it in a locked safe

2. Prover, who fulfils the requirements, has knowledge of the combination code and opens the locked safe

3. Prover returns the secret message to Verifier

4. Verifier is convinced that the prover really knows the combination code and can therefore be trusted‍

If this stranger is who she says she is, she would have knowledge of the combination code. Therefore she would be able to open the locked safe and find your secret message, which would prove to you that she is a trusted member of your group after all.

This is an analogy of how an interactive zero-knowledge proof works. Only those who are truly part of the group will have the secret combination code that gives them access to the locked safe, making it possible to prove their membership without giving anything else away.

Types of Zero-Knowledge Proofs

Zero-knowledge proofs come in two main types, each with its own characteristics and use cases:

Interactive Zero-Knowledge Proofs

Interactive zero-knowledge proofs involve a back-and-forth communication between the prover and the verifier. Through a series of exchanges, the prover convinces the verifier of the truthfulness of the statement without disclosing the underlying information. This dynamic interaction allows for real-time verification and adjustment, making it suitable for certain applications.

Non-Interactive Zero-Knowledge Proofs

In contrast, non-interactive zero-knowledge proofs are designed for scenarios where a single round of communication is preferred or required. The prover generates a proof, and the verifier can independently and efficiently verify it without the need for additional interaction. Non-interactive zero-knowledge proofs are often more practical in situations where real-time communication is challenging or not desired.

When it comes to ZKP implementation, there are two main approaches that have given rise to the two most popular types of zero-knowledge proofs – zk-SNARKS and zk-STARKs. Both approaches have shown promise and attracted significant interest, which has naturally sparked a somewhat of a SNARKs vs STARKs debate. However, the main thing here is that both of these models are demonstrating the power of ZKPs and are already having practical applications

Zk-SNARKs

Succinct non-interactive argument of knowledge, or SNARK, is a type of zk-proof that was first popularized by privacy protocols like Zcash and Monero. Zk-SNARKs are often described as “zero-knowledge proofs that require a trusted setup to generate the keys used to create and validate the proofs”. The problem with this definition is that it too is kind of vague. What is that trusted setup and what exactly are those keys? Well, to answer these questions we need to go back to our jar of balls.

So in our ZKP example, the prover and the verifier worked together to create a proof. They interacted with one another. This is because zero-knowledge proofs, as they were originally conceived, are inherently interactive. But wait, we just said that the ‘N’ in SNARK stands for “non-interactive”. Well yes, this is the key distinction that transforms zero-knowledge proofs from purely theoretical constructs into an actual technology with practical applications.

In the case of our very simple example, generating a proof is a relatively straightforward process that requires just a few rounds of prover-verifier interaction. But if we want to do something practical, the complexity of interaction could skyrocket, with countless rounds of back and forth between prover and verifier. And if that wasn’t enough, a proof generated this way is only good for the verifier that has participated in the interaction, meaning that this laborious process has to be repeated for each new verifier. You cannot do anything at scale in this way.

The non-interactive approach circumvents these limitations in an ingenious way. It requires a common reference string (CRS) – the ‘key’ in our definition – to be shared between prover and verifier. The shared CRS allows the prover to demonstrate their knowledge of some information without revealing what that information is and without directly interacting with the verifier. Instead, the prover runs the information through a special algorithm designed to compute a zk-proof. Then the verifier receives the ZKP and runs a different algorithm to verify its validity. Most importantly, this method ensures that anyone who has access to the CRS and the verifying algorithm can become a verifier. This is why the CRS is often referred to as the public parameters of the system.

So with the zk-SNARK approach, the CRS is generated during an initial setup phase. During that phase, some random number values are generated and then encrypted to create the CRS. Once generated, the CRS can be used in perpetuity to generate SNARKs for that system without direct interaction between prover and verifier. And, because we skip all that back and forth communication between prover and verifier, we can generate zero-knowledge proofs that are short enough – succinct, if you will – to be stored on a blockchain. It should be noted that ‘succinct’ is not just a generic term, but it has a specific meaning in the context of zk-proofs. If a ZKP is succinct it means that it is shorter than the witness.

The random number values that are generated during the initial setup are what we call secret randomness or ‘toxic waste’. It’s paramount that they remain secret, because if they are compromised, they could be used to generate false proofs. So, in order to ensure that this doesn’t happen, the party performing the setup must destroy the toxic waste after the CRS generation. And we can only be sure that that party has acted honestly if we have a trusted setup. We have to trust that the party performing the setup has acted honestly.

The requirement for a trusted setup is seen as the main drawback of SNARKs, with critics pointing out that it runs counter to the trustless and decentralized nature of Web3. The lack of such a requirement is often cited as the biggest advantage that STARKs have over SNARKs.

To mitigate this criticism, most zk-SNARK protocols perform trusted setup via multi-party ceremonies. As the name suggests, in these ceremonies multiple participants (the number can be in the hundreds, depending on the particular ceremony) work together to generate the common reference string. Each participant works with their own portion of the toxic waste that remains secret to the other participants. Through the magic of a certain subfield of cryptography called multi-party computation (MPC), the participants are able to jointly compute the CRS.

The great thing about multi-party ceremonies is that if even one of the participants acts honestly, we can be sure that the secret randomness cannot be exposed. And with modern ceremonies often involving up to hundreds of participants, we can say that the setup is practically trustless.

Still, there’s another approach to generating zk-proofs, one that uses a novel breakthrough in cryptography to ensure that the process is completely trustless.

Zk-proofs use cases

While zk-proofs are a nascent technology in the context of Web3, developers are already finding interesting ways to use the technology in the space. So far several strong use cases have emerged.

Scalability

Due to their succinctness, zk-proofs could be a massive gamechanger for blockchain scalability. In fact, ZKPs are at the heart of one of the most promising scaling technologies for Ethereum – zero-knowledge rollups. ZK rollup solutions use ZKPs to generate ‘validity proofs’ for entire batches of transactions that have been executed on a Layer 2 network. The validity proofs are then submitted to the Ethereum mainnet to be permanently added to the network’s transaction history. With this method we can execute thousands of transactions outside of Ethereum and submit the results back to the mainnet via a single transaction.

Privacy

The unique properties of zk-proofs make them ideal for privacy use cases and, it’s no surprise that the technology was first embraced by privacy-focused protocols like Zcash and Monero. But the possible applications of the tech are much more numerous. For example, ZKPs could be invaluable for enterprise-grade solutions, allowing companies to prove to their customers, business partners or industry regulators that they follow the correct procedures and processes without revealing sensitive information about their operations.

Interoperability

Zk-proofs could also be used to improve interoperability between different Web3 networks. We just discussed how zk rollups can help L1 and L2 networks to communicate efficiently and the same principle could be applied to improve the efficiency of cross-chain technology.

Conclusion

As we delve deeper into the exciting world of zero knowledge proofs, one thing becomes clear – the technology has incredible potential and warrants further research and development. It feels like we’ve only scratched the surface of what this technology is capable of. Of course, this is not to say that ZKPs are a miracle solution for every problem. After all, every technology has its limits. But as the Web3 community continues to explore the field, more and more ZKP applications are bound to emerge.

One of the most incredible things that researchers have learned about zero knowledge proofs is that every statement that has a proof also has a ZKP. The implications of this discovery are fascinating and it makes us confident that even though ZKP technology has its limits, its ceiling is incredibly high.